CAPITOLO 2

CARATTERIZZAZIONE PIEZOELETTRICA

2.1 TECNICHE DI ANALISI

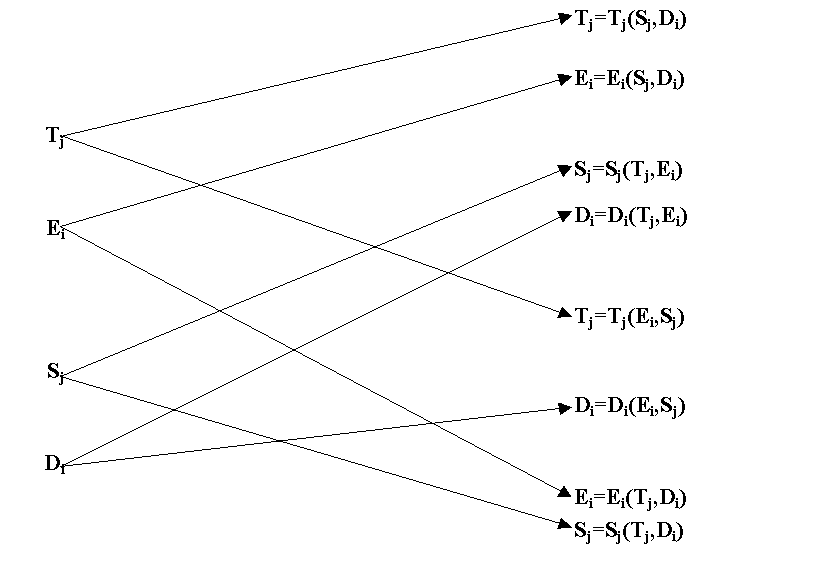
Come già precedentemente affermato, le proprietà dielettriche sono tra loro legate da variabili di stato del sistema, e quindi la scelta tra le variabili indipendenti per un sistema costituito da materiale piezoelettrico polarizzato e sottoposto simultaneamente ad uno stress (T_j) e a un campo elettrico (E_i), può essere arbitrariamente selezionata come mostrato in figura 2.1

Con:

i=1, 2, 3 e j=1,2,…6

Figura 2.1: Scelta delle variabili indipendenti

Lo studio delle caratteristiche elastiche, piezoelettriche e dielettriche di un materiale piezoelettrico consiste quindi nella determinazione dei valori delle numerose costanti precedentemente descritte.

A seconda delle costanti fondamentali che si vogliono determinare si richiede una serie di misure su campioni di diverse geometrie e dimensioni.

I metodi adottati, in generale, per la determinazione delle costanti sono due: uno basato su misure statiche e quasi statiche, l’altro basato sul metodo della risonanza in regime dinamico.

2.2 MISURE STATICHE E QUASI STATICHE

Si può subito dire, molto sinteticamente che, per quanto riguarda le misure quasi statiche, bisogna distinguere i due effetti, cioè quello diretto e quello inverso, in modo da poter ottenere la costante di carica piezoelettrica d_ij e lo strain meccanico subito dal materiale per unità di campo elettrico applicato, da indicarsi nuovamente con d_ji in due modi diversi (come già è stato detto precedentemente le due costanti sono numericamente uguali)

2.2.1 Effetto diretto

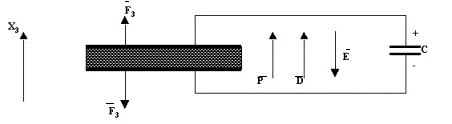
Figura 2.2: Grandezze e cariche in un campione sollecitato meccanicamente e con d₃₃>0

Nella figura 2.2 è mostrato, per maggiore chiarezza, un campione piezoelettrico polarizzato nella direzione dello spessore (asse x₃). Il campione è dotato di elettrodi sulle superfici maggiori ed il condensatore posto in parallelo deve avere una capacità C da 10 a 100 volte maggiore di quella del campione stesso.

Se al campione applichiamo uno sforzo di intensità T₃, parallelo alla direzione di polarizzazione, allora la forza F₃ (in modulo) risultante sul campione è data dal prodotto tra lo sforzo T₃ e l’area A della superficie su cui è applicato, ed ha stesso verso e direzione di T₃.

Il comportamento del materiale in questa situazione è descritto dall’equazione.

D₃=d₃₃T₃+e₃₃E₃^T                                                (2.1)

Tale equazione è stata ricavata dalla corrispondente equazione ponendo T₁ e T₂ uguali a zero.

La carica totale sulla superficie sottoposta a stress è:

 Q=D₃A                                         (2.2)

essendo D₃ lo spostamento elettrico in direzione 3.

Sul condensatore, di capacità C, risulta applicata la tensione di intensità:

 V=Q/C                                        (2.3)

L’intensità del campo elettrico indotto sulla direzione 3 vale:

E₃= - V/t                                       (2.4)

Dove t è lo spessore del campione.

Il modulo del vettore di polarizzazione corrispondente vale (sempre in direzione 3):

P₃=D₃ - e₀E₃                                                         (2.5)

Poiché la grandezza normalmente misurata è la tensione V, risolvendo le equazioni precedentemente scritte secondo tale variabile si ottiene:

                                     (2.6)

 La (2.6) può essere semplificata (cosa che realmente si fa) in questo modo:

se 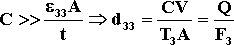            (2.7)

Quindi dalla (2.6) si deduce che:

1.     Se      d₃₃>0 e T₃>0   Þ  V>0 cioè si individua il verso positivo degli assi cartesiani ovvero degli assi cristallografici.

2.     Se è valida la (2.7) è come se lavorassimo con campo elettrico nullo e stress costante (la (2.1) si potrebbe scrivere: D₃=d₃₃T₃ o più in generale D_i=d_ijT_j)

2.2.2 Effetto inverso

In questo caso si considera un campione sottoposto a campo elettrico costante (o lentamente variabile) e uniforme e si misura lo strain che ne consegue.

In condizioni di stress nullo otteniamo la relazione:

S_j=d_ijE_i                                       (2.8)

La condizione di campo elettrico costante e uniforme è facilmente ottenibile, mentre lo stress nullo si può garantire mediante opportune geometrie del campione.

L’uso dell’effetto inverso permette una maggiore accuratezza nella determinazione delle costanti piezoelettriche ma presenta maggiori difficoltà nella rilevazione della grandezza da misurare in quanto gli strain prodotti da campi elettrici anche elevati possono essere molto ridotti.

A tale riguardo è interessante citare la tecnica di rilevazione acustoottica interferometrica [7]. Tale tecnica consiste nell’indirizzare un fascio laser di frequenza e intensità note sul campione mentre questo viene sottoposto ad un campo elettrico alternato.

La deformazione periodica del campione provoca una modulazione di fase del fascio riflesso. Tale fascio riflesso viene fatto interferire con una parte del fascio incidente opportunamente deviato. La sovrapposizione dei due fasci agisce su di un fotorivelatore che fornisce in uscita un segnale modulato in fase dalla frequenza di oscillazione del campione. Operando opportuni filtraggi di questo segnale si può risalire all’ampiezza di oscillazione del campione e quindi alle sue caratteristiche di elasticità.

Il segnale elettrico che sollecita il campione opera al di sotto delle frequenze di risonanza del campione e pertanto si può parlare di misure quasi statiche. Con questo metodo è possibile determinare ad esempio la costante d₃₃ e tutte le costanti con pedice (33).

L’uso di questa tecnica in unione a quella dinamica, che verrà descritta in seguito, può semplificare la misura delle costanti del materiale in quanto consente di evitare la realizzazione dei campioni più critici e complessi, come quelli da polarizzare nel senso della lunghezza.

In generale le tecniche di misura statiche e quasi statiche consentono una precisione abbastanza buona con errori dell’ordine di qualche punto percentuale. Le tecniche di misura più utilizzate tuttavia sono quelle in regime dinamico, che forniscono una precisione maggiore e si possono applicare più facilmente a classi più ampie di orientamenti cristallografici e geometrie di campioni.

2.3 MISURE IN REGIME DINAMICO: CIRCUITO EQUIVALENTE

Per effettuare le misure delle costanti piezoelettriche in regime dinamico è necessario utilizzare il metodo della risonanza. In pratica si tratta di sottoporre i campioni piezoelettrici a forze oscillanti con una pulsazione w ed una ampiezza F₀ in modo da porli in condizioni di risonanza.

In questo ambito è possibile ottenere misure significative sulla base della teoria inerente il modo di vibrazione del materiale, per cui bisogna realizzare i campioni secondo forme ben precise in modo da selezionare determinati modi di vibrazione[8].

Con il metodo della risonanza viene misurata l’impedenza elettrica del campione, detto anche risonatore, in funzione della frequenza del segnale che lo pone in vibrazione.

Il circuito equivalente di un campione piezoelettrico metallizzato su due facce piane e parallele di superficie A [m²], distanti tra loro t [m], vicino alla sua frequenza di risonanza, se il modo di vibrazione in esame è isolato, è costituito da un’induttanza L, da una resistenza R, e da una capacità C in serie tra loro e a loro volta in parallelo ad un’altra capacità C₀, come mostrato in figura 2.3

Figura 2.3: Circuito elettrico equivalente di un materiale piezoelettrico nell’intorno della sua frequenza di risonanza.

 Il parametro C₀ rappresenta la capacità effettiva della ceramica, mentre i parametri associati a L, C, R rappresentano rispettivamente la massa, l’elasticità e la dissipazione meccanica del risonatore.

Il reciproco dell’impedenza elettrica Z(W) [W] che esprime l'ammettenza in termini vettoriali in funzione della pulsazione del circuito in figura è:

          (2.9)

Dalla (2.9), ponendo successivamente:

 ,     ,         ed               (2.10)

Si ottiene:

         (2.11)

Quindi:

                     (2.12)

Infine, normalizzando la (2.12), si può scrivere:

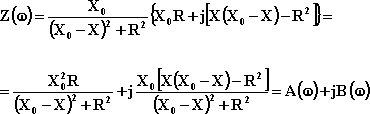            (2.13)

essendo A(w) la parte reale (o componente resistiva o resistenza) e B(w) il coefficiente dell’immaginario (o componente reattiva o reattanza) del vettore impedenza Z(w).

Dalla (2.10) si ricava innanzi tutto che A(w)>0 sempre, mentre si ha B(w)=0 (pulsazione di reattanza nulla) se e solo se :

   cioè quando      (2.14)

Poiché nella pratica sperimentale, nei materiali piezoelettrici, si può trascurare il valore della resistenza R rispetto alla reattanza capacitiva X₀, almeno nelle vicinanze di X=0, allora le soluzioni della (2.14) potrebbero essere:

      e       ;                      (2.15)

da cui, ricordando le posizioni espresse in (2.10) si avrà:

      ed      ,         (2.16)

essendo C^’ il valore della capacità C e C₀ in serie tra loro. Siccome in generale, nei materiali piezoelettrici, il valore di C₀ è più grande di C, i valori numerici di w₁ e w₂ saranno tra loro vicini, pur essendo comunque sempre w₂ - w₁ >0

In definitiva possiamo quindi affermare che w₁ è la pulsazione di risonanza del campione in esame e dipende solo dalle caratteristiche fisiche e meccaniche di questo; la frequenza di risonanza f_r, o frequenza di risonanza serie, sarà allora f_r=w₁/2p; mentre w₂ è la pulsazione di antirisonanza del campione; tale pulsazione che, essendo funzione anche di C₀, dipenderà dai parametri geometrici del campione. Analogamente a prima, la frequenza di antirisonanza f_a, o frequenza di risonanza parallelo, sarà f_a=w₂/2p.

Nella figura 2.4 sono riportati gli andamenti caratteristici (in unità arbitrarie) della parte reale A(w) e della parte immaginaria B(w) (modulo e fase) dell’impedenza Z in funzione della pulsazione w e relativi ad un circuito come quello di figura 2.3.

Quindi, come già fatto notare, le frequenza di risonanza e antirisonanza sono in relazione con le caratteristiche meccaniche e fisiche e quindi con le proprietà dielettriche, piezoelettriche ed elastiche del materiale. E’ necessario, quindi, misurare tali frequenze per risalire ai coefficienti ricercati.

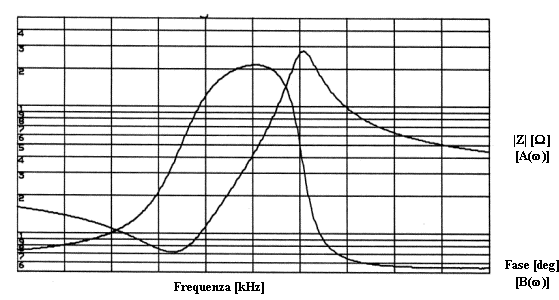
Figura 2.4: andamenti caratteristici delle funzioni A(w) e B(w)

 L’approssimazione effettuata nella (2.15) è corretta se si tengono presenti le seguenti considerazioni:

1.     Come già precedentemente detto, allo scopo di caratterizzare elettricamente una ceramica piezoelettrica, bisogna utilizzare campioni di forme diverse, polarizzati lungo direzioni prestabilite. Il diverso numero di campioni di forme particolari è necessario per fare un’analisi del comportamento elettrico di una ceramica polarizzata, lungo una direzione per volta (detta analisi unidimensionale), osservandone il modo di vibrazione fondamentale (o modo di vibrazione puro).

2.     Ci si occupa allora della ricerca di particolari frequenze caratteristiche, tramite il metodo noto come “metodo della risonanza”, applicando ai campioni un opportuno campo elettrico e variandone la frequenza.

3.     I campioni di forme e dimensioni standardizzate vengono caratterizzati con un analizzatore di impedenza e di guadagno/fase (mod. Hewlett Packard 4194A) mediante il quale si registra l’andamento del modulo e della fase dell’impedenza nell’intervallo di frequenza 100 Hz - 15 MHz.

4.     Si trovano tre frequenze nell’intorno della frequenza di risonanza e tre nell’intorno della frequenza di antirisonanza e cioè:

f_m= frequenza di minima impedenza

f_s= frequenza di risonanza serie o di minima resistenza assoluta

f_r= frequenza di risonanza

f_n= frequenza di massima impedenza

f_p= frequenza di risonanza parallelo o di massima resistenza assoluta

f_a= frequenza di antirisonanza

5.       Come già detto, le frequenze f_S e f_p sono indipendenti dai parametri del circuito equivalente a costanti concentrate, esse fanno infatti riferimento a conduttanza e resistenza assoluta del materiale piezoelettrico.

La differenza tra f_p e f_s dipende sia dal “fattore di merito” del materiale, definito come:

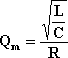                                     (2.17)

sia dalla geometria del risonatore.

6.     Introducendo il fattore di accoppiamento elettromeccanico effettivo k²_eff , definito come:

                                (2.18)

si può definire la figura di merito M, che mette in relazione il fattore di qualità meccanica (o fattore di merito) Q_m e il fattore di accoppiamento elettromeccanico effettivo:

                                 (2.19)

7.     Le frequenze da misurare dovrebbero essere f_s e f_p, ma è possibile sostituirle con f_m e f_n rispettivamente; ciò rende più semplice il procedimento di misura in quanto tramite un HP4194 impedence/gain-phase analyzer è possibile, tra le altre numerose funzioni, avere uno sweep in frequenza dell’impedenza del campione in esame [9].

8.     In definitiva le approssimazioni di cui sopra sono possibili nel caso in cui il valore della figura di merito M sia maggiore di 50. In tal caso infatti, le distanze tra le frequenze si riducono a tal punto da poter approssimare f_s con f_m e f_p con f_n. Nel caso in cui il fattore M sia minore di 50 occorre fare delle correzioni sulle quantità misurate o fare misure più dettagliate con un ponte di impedenza o ammettenza, per determinare f_p e f_s direttamente; se tuttavia il valore di M è così piccolo da essere minore di 5 non è possibile fare misure accurate di f_p.[10].

2.4 CARATTERIZZAZIONE DI UN MATERIALE PIEZOELETTRICO

Per quanto riguarda la caratterizzazione completa di un materiale piezoelettrico bisogna tener presente la teoria della propagazione delle onde nella particolare geometria dei campioni in esame.

Per poter calcolare quindi le costanti piezoelettriche, il modo più semplice è di effettuare misure di risonanza su geometrie particolari, allo scopo di isolare i modi di vibrazione, e quindi poter calcolare una sola costante alla volta, o almeno un set limitato di costanti piezoelettriche.

Si possono usare diverse combinazioni di forme per ottenere il set di costanti indipendenti, ma la più usata è la seguente [5]:

A.   Piastra rettangolare

B.    Piastra quadrata

C.   Disco

D.   Parallelepipedo allungato “shear-plate”

E.    Parallelepipedo allungato

2.4.1 Caratterizzazione piezoelettrica: metodi di misura [11]

Se lo strain e lo spostamento elettrico sono, ad un certo istante, le variabili di stato indipendenti di un sistema piezoelettrico, allora le equazioni da considerare sono:

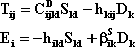                       (2.20)

dove i, j, k, l=1, 2, 3 ed inoltre si assume che:

1.     T_ij, S_kl, sono i tensori di stress e strain. In particolare lo strain è messo in relazione con lo spostamento meccanico `u(x₁, x₂, x₃) attraverso la seguente relazione:

                               (2.21)

 2.     E_i e D_k sono i componenti del campo elettrico e dello spostamento elettrico lungo le direzioni i e k che verificano, rispettivamente, le seguenti relazioni:

               e                  div `D=0

     dove `V è la differenza di potenziale tra due facce del materiale piezoelettrico

3.     C^D_ijkl, h_hij, b^S_ik sono rispettivamente i componenti tensoriali della rigidità elastica, piezoelettricità e l’inverso della permettività. Per un piezoelettrico polarizzato lungo l’asse x₃ la matrice elasto-piezo-dielettrica ha 5, 3 e 2 componenti, rispettivamente, non nulli.

4.     Un onda piana, in generale ha la seguente forma:

                          (2.22)

     dove U_i è il componente dell’ampiezza dello spostamento lungo l’asse i;

     n è la velocità di propagazione dell’onda nel mezzo;

     n_j denota la direzione della propagazione dell’onda.

     Inoltre bisognerà tenere presente la legge di Newton:

                              (2.23)

     dove r è la densità del materiale e t è il tempo

5.     I materiali piezoelettrici sono dotati di simmetria cristallina di classe ¥-mm equiparabile a quella della classe 6-mm. Inoltre gli assi cartesiani di riferimento saranno posti lungo le direzioni dei modi di vibrazione “puri”

 2.4.1.1: Modo di vibrazione di un parallelepipedo piezoelettrico

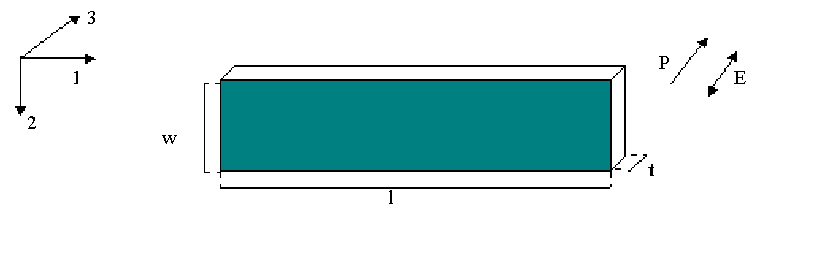
Nella figura 2.5 sono state definite le convenzioni sul sistema di riferimento, sulle dimensioni e sullo stress applicato su di un parallelepipedo piezoelettrico, in cui sono state applicati gli elettrodi sulle facce maggiori e il verso della polarizzazione è quello indicato (lungo l’asse x₃).

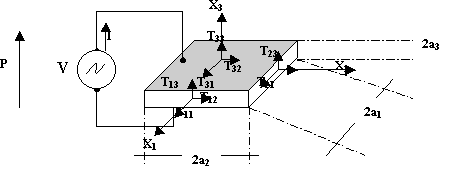
Figura 2.5: Convenzione sul sistema di coordinate cartesiani, sulle dimensioni e sullo stress

Applicando una tensione alternata (`V) sulle facce maggiori del parallelepipedo piezoelettrico, si avrà una vibrazione del parallelepipedo stesso e quindi uno spostamento `u lungo i tre assi cartesiani x_i, con i=1, 2, 3.

La vibrazione lungo l’asse i può essere scritta nel seguente modo:

                              (2.24)

dove  e n_i è la velocità dell’onda lungo l’asse x_i, w è la pulsazione della vibrazione.

Quindi tenendo presente la figura 2.5 e le equazioni (2.24) e (2.21) si possono fare le seguenti considerazioni:

-      I componenti del tensore di strain S_ij (i¹j) sono nulli: cioè S₄=S₅=S₆=0.

-      Poiché la tensione alternata è applicata sulle due facce parallele distanti tra loro 2a₃, il campo elettrico sarà perpendicolare a tali facce e quindi sarà solo E₃¹0 (E₁=E₂=0)

-      La (2.20) viene semplificata, perché: E₁=E₂=0, e D₁=D₂=0, perché S₄=S₅=0 e di conseguenza anche T₄=T₅=T₆=0, quindi il set completo di equazioni in questo caso sarà:

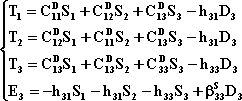                 (2.25)

Considerando la (2.25), l’equazione div `D=0 e la (2.24) si ha:

                                 (2.26)

 dove r è la densità del materiale e dove si trova che

    e    

Le velocità n₁  e n₂ (in modulo) sono uguali perché il piano x₁-x₂ è isotropo per la piezoelettricità.

E’ da notare, inoltre, che in un mezzo illimitato le velocità n₁ e n₂ sono diverse. Nel caso in esame il mezzo è limitato e le onde che giacciono sul piano x₁ – x₂ sono creati da un’onda che si propaga lungo l’asse x₃; nei mezzi illimitati le onde sono create e si propagano lungo l’asse x₁ (o x₂) e non ci sono onde lungo l’asse x₃.

Se la tensione alternata `V ha una frequenza vicino a quella di risonanza del parallelepipedo piezoelettrico allora possiamo determinare l’impedenza del risonatore in esame. Infatti possiamo scrivere, sempre in riferimento alla figura 2.5, che:

 quindi:

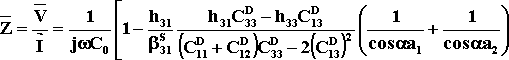
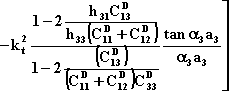    [2]

dove:

                       con i=1,2,3                           r è la densità del parallelepipedo piezoelettrico.

A questo punto si può concludere che se si vuole solo la vibrazione trasversale (solo sul piano x₁-x₂) su di un parallelepipedo piezoelettrico sottoposto ad una tensione alternata allora deve essere:

            e       

    oppure        

 con n=1, 2, 3, ….  e l è la lunghezza d’onda della tensione applicata: ciò significa avere 2a₁ oppure 2a₂ uguali a (2n+1)l/2 ovvero una delle due dimensioni perpendicolari a x₃ devono essere un numero dispari di l/2.

Il procedimento fin qui adottato si può estendere, in modo analogo, a tutte le forme di tipo parallelepipedo e quindi trovare le dimensioni adeguate per ottenere modi di vibrazione puri di tipo trasversale e longitudinale e quindi i vari componenti della matrice elasto-piezo-dielettrica.

E’ da osservare che per ottenere la caratterizzazione completa è necessario, come precedentemente detto, anche una forma circolare per avere un modo di vibrazione puro detto “vibrazione planare” (per la dimostrazione si faccia riferimento a [11]e[12]).

Tabella 2.1: parametri e unità di misura

 Riassumendo, e tenendo conto della tabella 2.1, le cinque forme standard per la caratterizzazione completa di un materiale piezoelettrico sono:

A.   Piastra rettangolare

La piastra rettangolare deve presentare le seguenti specifiche geometriche affinché la vibrazione risultante sia solo trasversale:

           l >3,5w

          l >3,5t

Si misurano f_s e f_p alla frequenza di risonanza fondamentale in lunghezza e si effettuano poi i seguenti calcoli:

        s₁₁^E=1/(4rf_s² l²)                                                              (1.A)

        k₃₁²/(1-k₃₁²)=(p/2)(f_p/f_s)tan((p/2)Df/f_s)                         (2.A)

        s₁₁^D=(1-k₃₁²)s₁₁^E                                                (3.A)

        d₃₁=k₃₁(e₃₃^Ts₁₁^E)^1/2                                                        (4.A)

        g₃₁=d₃₁/e₃₃^T                                                                    (5.A)

 dove Df=f_p-f_s e il coefficiente e₃₃^T verrà ricavato dalla (6.B).

B.   Piastra quadrata

La specifica del campione dovrà essere in questo caso:

          l >10 t.

Si misura quindi la capacità a bassa frequenza C_l,f, ad alta frequenza C_h,f, le frequenze di risonanza f_s e f_p del modo di vibrazione in spessore e la frequenza di risonanza parallelo di una delle armoniche della vibrazione in spessore f_p,i (con i=1,3,5,7...); è così possibile calcolare:

           e₃₃^T=C_1,ft/l²                                                                   (6.B)

          e₃₃^S=C_h,ft/l²                                                                     (7.B)

          k^t₃₃²=(p/2)(f_s/f_p)tan((p/2)Df/f_p)                                      (8.B)

          C₃₃^D=4r(f_p,it/i)²                                                                           (9.B)

C₃₃^E=C₃₃^D(1-k^t₃₃²)                                                         (10.B)

          d₃₃=k^t₃₃(s₃₃^Ee₃₃^T)^1/2                                                      (11.B)

 dove r è la densità del materiale, i è l’ordine dell’armonica e s₃₃^E si ricaverà dalla relazione (31.E).

 Vengono misurate, oltre alle grandezze già dette, le frequenze di risonanza serie fondamentale f_III, f_IV; dal loro rapporto e usando la tabella riportata sugli standard [12] è possibile avere una stima del coefficiente di Poisson:

 f_III/f_{IV Þ sp}

Poiché

          s_p=-s₁₂^E/s₁₁^E                                                                                             (12.B)

          Þ  s₁₂^E=-s_ps₁₁^E                                                                                          (13.B)

 s₁₁^E è stata calcolata nella relazione (1.A).

 Inoltre misurando l’impedenza minima Z_s alla frequenza di risonanza e la capacità C_l,f  a bassa frequenza si ricava:

           Q_m= f_p²/(2pf_s Z_sC_l,f (f_p²-f_s²))                       (14.B)

C.   Disco

La specifica dovrà essere, nel disco:

           d >10t

Si misurano quindi f_s e f_p del modo di vibrazione planare e si calcolano i seguenti coefficienti:

k_p²/(1-k_p²)=((1-s_p)J₁(h₁(1+Df/f_s))-h₁(1+Df/f_s)J₀(h₁(1+Df/f_s)))/((1+s_p)J₁(h₁(1+Df/f_s))) (15.C)

dove:

          J₀, J₁® funzioni di Bessel

          h₁ ® soluzione positiva dell’equazione: (1+s_p)J₁(h)=hJ₀(h)

Una volta che sia noto s_p, ricavare sia k_p che h₁ è più semplice di quanto possa sembrare in quanto, senza dover risolvere le equazioni sopra scritte, è possibile trovare negli standard il grafico dell’andamento di k_p in funzione di Df/f_s al variare di s_p, nonché le tabelle relative ai valori che assume h₁ al variare sempre di s_p.

Dalla geometria a disco è possibile inoltre calcolare:

           k₃₁²=k_p²(1-s_p)/2                                                           (16.C)

          s₁₁^E=h₁²/(p²d²f_s²(1-s_p²)r)                                           (17.C)

          d₃₁=k₃₁(e₃₃^Ts₁₁^E)^1/2                                                     (18.C)

          g₃₁=d₃₁/e₃₃^T                                                                  (19.C)

D.   Parallelepipedo allungato, “shear plate”

Specifiche del campione saranno in questo caso:

          l >3w

          l >3t

Si misurano a questo punto le capacità a bassa e alta frequenza (C_l,f e C_h,f rispettivamente) e una delle frequenze f_p,i corrispondente ad una delle armoniche di ordine superiore (con i=1,3,5,7...). E’ così possibile ricavare:

          e₁₁^T=C_l,ft/(lw)                                                              (20.D)

         e₁₁^S=C_h,ft/(lw)                                                              (21.D)

          k₁₅²=1-(e₁₁^S/e₁₁^T)                                                         (22.D)

          s₅₅^D=(i/(f_p,it))²1/(4r)                                                     (23.D)

          s₅₅^E=s₅₅^D/(1-k₁₅²)                                                          (24.D)

          d₁₅=k₁₅(e₁₁^Ts₅₅^E)^1/2                                                      (25.D)

          g₁₅=d₁₅/e₁₁^T                                                                   (26.D)

          s₄₄^D=s₅₅^D                                                                       (27.D)

          C₄₄^E=1/s₄₄^E                                                                   (28.D)

          C₄₄^D=1/s₄₄^D                                                                  (29.D)

E.   Parallelepipedo allungato

Poste le specifiche del campione:

          l >3w

          l >3t

Si misura la frequenza di risonanza f_p del modo di vibrazione in lunghezza e si ricavano i seguenti coefficienti:

          s₃₃^D=1/(4rf_p²l²)                                                            (30.E)

          s₃₃^E=s₃₃^D/(1-k₃₃²)                                                          (31.E)

La simmetria del cristallo [6] piezoelettrico ci permette, inoltre, di ricavare dalle relazioni esistenti tra le costanti elastiche.

Usando la relazione C₃₃^E=(s₁₁^E+s₁₂^E)/(s₃₃^E(s₁₁^E+s₁₂^E)-2(s₁₃^E)²) si ha che:

           (s₁₃^E)²=1/2(s₁₁^E+s₁₂^E)(s₃₃^E-1/C₃₃^E)                               (32.E)

          C₁₃^E=-s₁₃^EC₃₃^E/(s₁₁^E+s₁₂^E)                                            (33.E)

          C₁₁^E=1/2(s₃₃^EC₃₃^E/(s₁₁^E+s₁₂^E)+1/(s₁₁^E-s₁₂^E))                (34.E)

          C₁₂^E=s₃₃^EC₃₃^E/(s₁₁^E+s₁₂^E)-C₁₁^E                                     (35.E)

I coefficienti così ricavati vengono quindi tabulati e forniti come caratteristiche piezoelettriche del materiale; c’è da aggiungere che solitamente nelle tabelle vengono forniti i valori delle costanti dielettriche relative, anziché i valori di quelle assolute. Per esempio, invece di e₁₁^T viene dato K₁^T=e₁₁^T/e₀ dove e₀ è la permettività elettrica del vuoto.

2.5 PROPRIETA’ ACUSTICHE

Molto importanti in alcuni specifici settori applicativi sono le proprietà acustiche dei piezoelettrici. Qui interessano, però, le analogie che le onde acustiche di un materiale piezoelettrico hanno con le grandezze elettriche. A tale proposito è necessario fornire brevi cenni di fisica acustica. [13]

Come noto le onde sonore in un mezzo sono originate da vibrazioni delle particelle del mezzo attorno alla loro posizione di equilibrio. Il diffondersi della vibrazione di una particella alle particelle vicine provoca la propagazione dell’onda sonora del mezzo. Quando l’onda viene trasmessa nella stessa direzione della vibrazione si originano delle compressioni e rarefazioni alternate nel mezzo, da cui il nome di onde di compressione. Diversamente, quando il moto vibratorio è perpendicolare alla direzione di propagazione si originano le onde trasversali.

Il passaggio di un’onda sonora in un mezzo è caratterizzato da vettori d’onda, i cui valori variano periodicamente sia nel tempo sia nello spazio. I vettori più importanti sono:

 a)     spostamento (della particella) `x, che è lo spostamento dalla posizione di riposo di una singola particella del mezzo

b)    velocità (della particella)  che è la velocità con cui la particella si muove intorno alla posizione di riposo

c)     pressione acustica (o stress) `p, che è la pressione (o lo stress) dovuti all’azione dell’onda

 Per un’onda piana i vettori d’onda, in un dato istante, sono costanti in tutti i punti appartenenti ad un piano perpendicolare alla direzione di propagazione.

La velocità di propagazione dell’onda nel mezzo dipende dalle proprietà elastiche del mezzo oltre che dalla sua densità. Mediante opportune considerazioni si giunge ad affermare che:

                                     (2.27)

In questa espressione si è indicato con c la velocità di propagazione dell’onda, r la densità del mezzo, Y^E il modulo elastico. Nel caso del materiale piezoelettrico descritto nel capitolo precedente si ha che Y^E corrisponde a   da cui:

                                   (2.28)

Una volta definiti i vettori d’onda e la velocità di propagazione dell’onda è possibile stabilire una analogia formale tra le vibrazioni di tipo acustico e quelle di tipo elettrico. Questo consente di considerare equivalenti le seguenti grandezze:

pressione acustica Û differenza di potenziale

spostamento Û carica elettrica

velocità Û corrente

questa analogia porta a definire l’impedenza acustica `Z_a, allo stesso modo dell’impedenza elettrica, come il rapporto tra pressione acustica e velocità:

           Û    

Analogamente a quella elettrica, anche l’impedenza acustica è rappresentabile da un numero complesso esprimibile come:

`Z_a=R_a+jX_a

in cui si distinguono la componente resistiva R_a e quella reattiva X_a.

Nel caso di onde piane in un mezzo privo di assorbimento i vettori `p e   hanno espressioni tali da poter esprimere Z_a nel seguente modo:

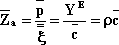
In questo caso, quindi, l’impedenza acustica risulta puramente resistiva e facilmente calcolabile.

L’unità di misura di questa grandezza è il rayl definito come segue:

[Z_a]=[rc]=[(kg/m³)(m/s)]=[kg/(m²s)]

Una volta definita l’impedenza acustica si possono introdurre due parametri che rivestono notevole importanza in campo applicativo cioè il coefficiente di riflessione a_r e il coefficiente di trasmissione a_t.

Data una coppia di materiali 1 e 2 in contatto tra loro lungo una superficie piana, si consideri un’onda sonora originata nel mezzo 1 incidente la superficie di separazione. L’energia sonora verrà una parte riflessa nel mezzo 1 e in parte trasmessa nel mezzo 2.

In corrispondenza della superficie di separazione il coefficiente a_r è definito dal rapporto tra l’intensità acustica dell’onda riflessa e quella dell’onda incidente, mentre a_t è il rapporto tra l’intensità dell’onda trasmessa e quella incidente. Se R₁ e R₂ sono le impedenze acustiche (reali) dei due mezzi si ha:

Queste equazioni mostrano che qualora, R₁ e R₂ siano uguali tra loro, a_t raggiunge il valore massimo che è 1, mentre a_r diventa nullo. In questa condizione ideale si ottiene il massimo trasferimento di energia da un mezzo all’altro. In pratica si possono ottenere buoni accoppiamenti acustici fra i due mezzi quando le due impedenze acustiche sono dello stesso ordine di grandezza [12].